益智数学游戏
你是否曾被那些看似简单却让人欲罢不能的益智数学游戏所吸引?你是否想过,在轻松愉快的游戏中,竟然隐藏着提升数学素养的神奇力量?
就让我们一起走进这些益智数学游戏的世界,开始锻炼我们的数学思维能力,探索它们背后的奥秘吧!
魔方
游戏背景:
魔方是20世纪最有影响的100项发明之一,它是一种由26个小立方体组成的三维立体拼图,这些小立方体通过内部的轴相互连接,形成一个大的立方体。魔方的每个面上有9个小立方体,每个坐标轴方向上分为三层,每层都可以自由转动,通过层的转动改变小立方体在立方体上的位置。
游戏规则:
魔方的基本规则是将打乱的小立方体恢复到原始的状态,即每个面的颜色一致。具体来说,魔方由6个面组成,每个面都有中央块、角块和边块之分。中央块位于魔方的中心,角块位于魔方的四个角上,边块则位于魔方的边缘。玩家需要通过旋转魔方的各个部分,使得每个面的颜色均匀一致。
九连环

游戏背景:
九连环是我国的一种传统智力玩具,历史悠久,流传广泛,征服了古今中外无数爱好者,是中国传统文化中的一颗璀璨明珠,与七巧板、华容道并称为我国古代三大智力玩具。
游戏规则:
九连环由九个相互连接的环组成,这九个环套在一个中空的长形柄中。九连环的玩法是要将这九个环从柄上解下来。
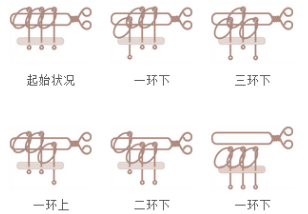
游戏技巧:
1.第一环可以在任何时候放上或取下环柄。
2.只有紧跟在领头环后的环可以放上或取下环柄。(领头环是套在柄上的最前面的环)
二进制游戏——猜姓氏

游戏背景:
猜姓氏是中国传统的一种社交游戏,而二进制是计算机科学中使用的数字系统。将这两者结合,可以创造出一种新颖的游戏体验,让玩家在享受游戏的同时,学习到二进制的应用和逻辑推理的技巧。
游戏规则:
1.提问者试图猜出回答者的姓氏。
2.提问者使用二进制的原理,通过一系列的提问来确定回答者的姓氏。
3.提问的问题为“此张卡中是否有您的姓氏?”,回答者只能回答是或否,即“是”对应1,“否”对应0。
4.提问者根据回答者的二进制回答,逐步构建出一个二进制数,这个数最终会被转换成对应的十进制数,从而揭示出回答者的姓氏。
24点

游戏规则:
参与游戏的人从扑克牌中抽出四张牌,用加、减、乘、除把牌面上的点数计算得到结果“24”,每个数字必须使用且仅能使用一次。扑克牌抽去大小王,J为数字11,Q为数字12,K为数字13,由主持人抽牌,每次4张,先答对者拥有该轮次4张牌,当公共卡池无牌后拥有最多卡牌数量的玩具获胜。如出现无法计算的情况,经所有玩家同意可放回公共卡池重新洗牌。
游戏举例:
扑克牌——3、6、6、Q
3×6+(12-6)=24
通关技巧:
刚开始玩这个游戏的时候,可以将J、Q、K三张牌抽去,因为增加了这三张牌,难度增加许多,并且出现无解情况的概率也提高了许多。(三年级以下可用1~10,三年级以上可加上J、Q、K)
四四呈奇

游戏规则:
用4个4,来表示出来1~100每个自然数。可以用的运算符号有: 加号、减号、乘号、除号、括号、小数点、循环节、根号、阶乘号以及数字的并列。
游戏举例:
1=44÷44 2=4÷4+4÷4
移棋相间

游戏规则:
将黑白棋子各n(n≥3)枚,左右分列成一行,○ ○ ○ … ○ ● ● ● … ● , 每次将相邻两子一并移至两个相邻空格之中,经n次移动使棋子变成连续排列的黑白相间形式 ● ○ ● ○ ● ○ … ● ○。(例如:3组黑白棋子则移动3次,4组黑白棋子则移动4次,以次类推)
游戏举例:
题目:○ ○ ○ ● ● ●
解法:○ ● ● ● ○ ○ 第一步
○ ● ● ○ ● ○ 第二步
● ○ ● ○ ● ○ 第三步
捡石子

游戏规则:
桌上放着m个棋子,家长和孩子轮流取走若干个,规定每人每次至少取走1个,最多取走n个,谁拿到最后一个棋子就赢得全部棋子。
游戏举例:
桌上放着15枚硬币,家长和孩子轮流取走若干枚,规定每人每次至少取走1枚,最多取走5枚,谁拿到最后一枚硬币就赢得全部硬币。
通关技巧:
在过程中观察规律,思考先手与后手的优势。
七巧板
游戏背景:
在《中国大百科全书》中,七巧板由宋代燕(宴)几图演变而来。黄柏思撰《燕几图》。明代严澄著《蝶几谱》将方形案几改为三角形,用13张三角形的案几合为蝶翅形,称为蝶翅几,也可拼出各种图形。清初始有七巧板。嘉庆养拙居士著《七巧图》刊行,使之流传。

游戏玩法:
七巧板是中国最古老的智力玩具之一,相传已有数千年的历史,在全国各地、各民族中都广泛流行。由一个正方形,五个三角形,一个平行四边形组成的七个小纸片(或者小木片、塑料片……),不但可以摆出千姿百态的飞禽走兽、山水草木、亭台楼阁……而且其中还蕴含着许多有趣的数学问题。
立体七巧板
游戏背景:
立体七巧板是丹麦人庇特·哈恩(Piet Hein)发明的。海森伯格在讲座上讲到宇宙可以分为一些立方体,这时哈恩突然灵感涌现,想到如果用不多于4个相同的小立方体通过面与面相连组成所有可能的“不规则”形状,把它们放在一起,是否能拼成一个大立方体?
几经努力,哈恩最后得出这样的不规则形状一共有7个,并用积木块和胶水做了出来,然后成功把它们拼成一个大立方体,证明了他的想法是对的。后来他以Soma的商标推出了他的发明作为玩具。
游戏玩法:
运用百变方块拼出立体七巧板的7个组块,再用7个组块拼成一个大立方体。将7个组块拼成一个大正方体,一共有480种不同拼法!
杨辉三角垛

游戏介绍:
杨辉三角垛是一种由20个小球堆积起来的金字塔形的正四面体,它由多层球体组成,每层的球体数量形成一个等差数列。
具体来说,最上层只有1个球,向下每层球体的数量依次增加,增加的数目等于该层的层数。例如,第二层有3个球,第三层有6个球,以此类推。这种排列方式类似于杨辉三角,因此被称为杨辉三角垛。
游戏规则:
将对应组块复原成正四面体。
烧脑十二块
游戏背景:
相传,“伤脑筋12块”的祖先是中国的骨牌,十二块不同形状的拼块可以拼出上千种形状,涉及数学中的几何学、拓扑学、运筹学、图论等多门学科。“伤脑筋的十二块”几乎是在国内外人士不约而同的研究下诞生的,“伤脑筋十二块”是中国人取的名字,它形象地说明了这种玩具的构造和功用。西方称为"中国的难题"或"潘多米诺(pentomino)骨牌"。
游戏玩法:
将12个拼块拼组成各种长宽的长方形,6×10有2339种拼法,5×12有1010种拼法,4×15有368种拼法,3×20只有2种拼法。
还可以将12个拼块拼成“回”字形,即边长是8×8,中间空2×2的正方形。
还可将12个拼块拼组成各种长宽高的长方体。3×4×5有3940种拼法,2×5×6有264种拼法,2×3×10有12种拼法。
数字华容道
游戏背景:
数字华容道源自中国传统的华容道游戏,最初是以三国时期的故事为背景,玩家需要通过移动棋子来帮助曹操逃出华容道。现代版本的数字华容道则简化了故事背景,变成了一个纯粹的数字拼图游戏。玩家需要将数字按照一定的顺序排列,通常是从小到大,形成一个有序的矩阵。
游戏规则:
1.玩家需要将数字按照从小到大的顺序排列,通常是从左上角的1开始,到右下角的最高数字结束。
2.玩家每次只能移动一个数字,且只能移动到相邻的空格上。
3.游戏的目标是在有限的移动次数内,将所有数字按照正确的顺序排列完毕。
数独
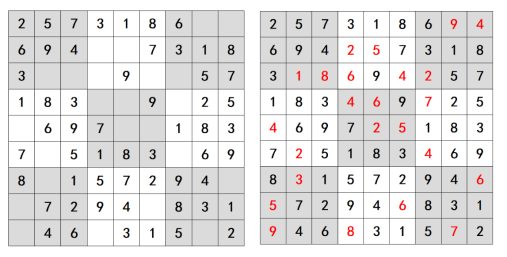
游戏背景:
数独”(Sudoku)一词源于日语, 18世纪末, 瑞士大数学家欧拉发明了这个游戏,后在美国发展,并在日本发扬光大。从2005年起,数独在西方国家风靡:数以千计的报纸提供数独游戏,电视上出现了数独节目,网上有了数独游戏软件……在英国,官方主办的《教师杂志》建议把数独引进课堂,因为它可以增进玩者的逻辑能力,开发大脑智力。
游戏规则:
9×9个格子里,已有若干数字,其它宫位留白,玩家需要自己按照逻辑推敲出剩下的空格里是什么数字,使得每一行、每一列、每一宫都有1到9的数字,并且一个数字在每个行列及每个小九宫格里都只能出现一次。
幻方
游戏背景:
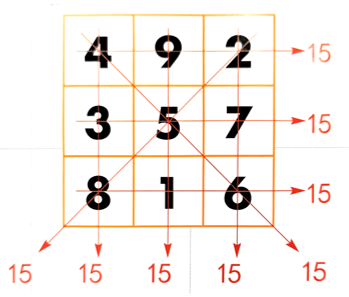
幻方是一种古老的数学游戏,据说最早可以追溯到中国古代。在中国,幻方被称为“洛书”,相传是大禹治水时发现的。幻方的特点是由一系列数字组成的正方形阵列,其中每行、每列以及两条对角线上的数字之和都相等。
游戏规则:
1.阶数:幻方的阶数指的是阵列的行数和列数,通常是奇数,如3x3、5x5、7x7等。
2.数字范围:幻方中的数字通常从1开始,连续到阶数的平方,例如3x3幻方的数字范围是1到9,5x5幻方的数字范围是1到25。
3.对称性:幻方的每行、每列和对角线上的数字之和必须相等。
4.唯一性:在给定的阶数和数字范围内,通常存在唯一的解。
游戏升级:
在横行、竖列个数均相同的方格内的空白格子中,填入不同整数,使得每横行、竖列、对角线之和都相等。
汉诺塔

游戏背景:
相传,上帝创造世界时作了三根金刚石柱子,在一根柱子上从上往下、从小到大顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一回只能移动一个圆盘,只能移动在最顶端的圆盘。有预言说,这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。
游戏规则:
1.汉诺塔有三根相邻的柱子,标号为A、B、C。A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。
2.每次只能移动一个圆盘,且每次只允许移动一个圆盘的位置。在任意一次移动中,较小的圆盘不可以被放在较大的圆盘下方。
3.汉诺塔游戏的目标是把A杆上的圆盘全部移到C杆上,并仍保持原有顺序叠好。